En el espectro Raman rotacional del H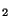 se han medido tres
líneas consecutivas, cuyo desplazamiento respecto a la frecuencia de
excitación es, respectivamente, de 814, 1033 y 1243 cm
se han medido tres
líneas consecutivas, cuyo desplazamiento respecto a la frecuencia de
excitación es, respectivamente, de 814, 1033 y 1243 cm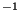 .
.
(a) Deducir las transiciones que han originado dichas líneas.
(b) Calcular la distancia internuclear del H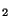 suponiendo que la
molécula es rígida.
suponiendo que la
molécula es rígida.
(c) Suponiendo que la molécula es no rígida, determinar
las constantes rotacionales 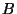 y
y 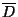 .
.
La curva de energía potencial del estado electrónico fundamental
de una molécula diatómica, A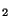 , viene dada por la
expresión:
, viene dada por la
expresión:
donde 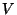 viene dado en cm
viene dado en cm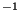 y
y 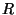 debe expresarse en Å. El peso
atómico de A es 10 g/mol.
Determinar:
debe expresarse en Å. El peso
atómico de A es 10 g/mol.
Determinar:
(a) La distancia de equilibrio.
(b) La constante rotacional.
(c) La constante de fuerza y frecuencia fundamental de vibración, y
(d) las energías de disociación 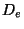 y
y 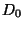 en kcal mol
en kcal mol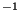 .
.
La Molécula de  Be
Be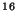 O presenta un sistema de bandas en la región
verde del espectro originado por la transición electrónica:
O presenta un sistema de bandas en la región
verde del espectro originado por la transición electrónica:
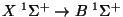 . Para la banda
. Para la banda
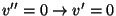 se han medido, entre otras, las siguientes
líneas de rotación consecutivas (en cm
se han medido, entre otras, las siguientes
líneas de rotación consecutivas (en cm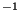 ):
21211.12, 21208.52, 21205.74, 21202.88, 21199.81,
21193.25, 21189.97, 21186.41,
21182.66 y 21186.88.
):
21211.12, 21208.52, 21205.74, 21202.88, 21199.81,
21193.25, 21189.97, 21186.41,
21182.66 y 21186.88.
(a) Determinar el origen de banda y la cabeza de banda.
(b) Determinar 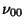 ,
, 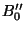 y
y 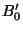 .
.
(c) Calcular 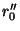 y
y 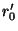 .
.
(d) Indicar hacia dónde estarán degradadas las bandas en esa transición
electrónica.
![]() viene dado en cm
viene dado en cm![]() y
y ![]() debe expresarse en Å. El peso
atómico de A es 10 g/mol.
Determinar:
debe expresarse en Å. El peso
atómico de A es 10 g/mol.
Determinar:
![]() y
y ![]() en kcal mol
en kcal mol![]() .
.