Espectroscopia de Llamas: Luminiscencia de intermediatos reactivos.

Objetivos

·          Obtener el espectro de emisión de una llama y conocer qué moléculas (intermediatos) se forman.

·          A partir del espaciado vibracional de las cabezas de banda del sistema Swan correspondiente a las transiciones d³Π_ga³Π_u de la molécula de C₂ obtener las constantes vibracionales ,,... y ,, ... de los estados electrónicos implicados en esta banda electrónica.

·          Obtener las energías de disociación D₀ de los estados d³Π_g y a³Π_u de la molécula de C₂ mediante el método de extrapolación lineal de Birge-Sponer.

·          Comparar las intensidades experimentales, de algunas bandas vibracionales del sistema d³Π_ga³Π_u de la molécula de C₂, con las intensidades teóricas.

·          A partir del espaciado rotacional de la rama P, de la banda ’=0- ”=0 del sistema B²Σ^-X²Π de la molécula de CH,  se obtendrán las correspondientes constantes rotacionales B_v’=0 y B_v”=0. Estimar también la temperatura de la llama mediante medidas espectroscópicas.

Introducción                                                            

Cualquier reacción de combustión (por ejemplo: propano o butano con oxígeno) se produce a través de un gran número de procesos elementales. En las llamas se forman diferentes moléculas diatómicas o radicales, tales como C₂, OH y CH en estados electrónicos excitados. Los espectros de estas moléculas se deben a transiciones electrónicas (UV-Visible) entre distintos estados vibracionales y rotacionales.

  

 

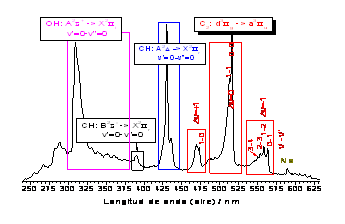
Figuras 1 y 2: Espectros de emisión en función de la longitud de onda y del número  de ondas.

 

En la figura superior derecha (Figura 1) se indica la zona donde aparecen las bandas electrónicas de las diferentes moléculas diatómicas (radicales) formadas en la llama: C₂: d³Π_g-> a³Π_u (banda Swan) con Δ Δ=-1, 0, 1; CH: A²Δ-> X²Π (’=0-”=0) y B²Σ^- ->X²Π (’=0-”=0) y  OH: A²Σ⁺-> X²Π (’=0-”=0). En la figura superior izquierda (Figura 2) se muestra el espectro de la llama obtenido con mayor resolución, donde ahora la escala en el eje de abcisas corresponde al número de onda (en cm^-1) en vacío.

Análisis de la estructura vibracional de la banda Swan  C₂:d³Π _ga³Π_u con Δv=-1, 0, 1

Las líneas espectrales de muchas moléculas no hidruros como C₂ se agrupan en secuencias de banda que corresponden a transiciones con igual Δ=’-”. Esto sucede cuando las constantes vibracionales de los estados electrónicos implicados no son muy diferentes (el espaciado vibracional es similar). Como resultado las transiciones con igual  Δ  aparecen  juntas  en  el espectro. La energía vibracional, en términos  de  energía  en

cm^-1 , se puede expresar como un desarrollo en serie:

                                                                                                                                 (1)

donde , ,…, son las constantes vibracionales (en cm^-1). Para transiciones de una misma banda electrónica, el espaciado entre niveles vibracionales adyacentes viene dado por 

                                                                                                           (2)

Si se consideran bandas con ’ constante (progresiones ’), a partir del espaciado entre bandas adyacentes donde cambia ”, se pueden obtener las constantes vibracionales del estado fundamental ,, etc. Si se consideran bandas con ” constante (progresiones ”), a partir del espaciado entre bandas adyacentes donde cambia ’, se pueden obtener las constantes vibracionales del estado excitado ,,etc. Para estos cálculos hay que utilizar la ecuación (2), aunque con el fin de simplificar el análisis, nos quedaremos únicamente con los dos primeros términos. En la Figura 3 se indica la asignación vibracional (cabezas de banda) que tomaremos como orígenes de banda debidos al sistema de bandas d³Π_ga³Π_u de la molécula de C₂.

(pincha aqui si quieres la tabla con los puntos y aqui si quieres la figura en pdf, en postscript o en gif)

 

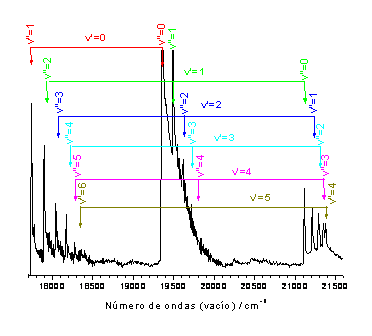
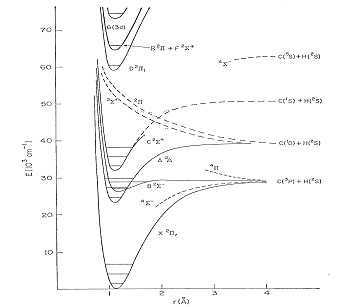
Figura 3: Asignación de las cabezas de banda del sistema d³Π_g -> a³Π_u del C₂.          Figura 4: Curvas de energía potencial del CH.

 

 

 

Ejercicio 1: Teniendo en cuenta esta asignación, a partir de los orígenes de banda medidos (en cm^-1) en el espectro dado, completar la tabla de Deslandres indicada a continuación para el sistema d ³Π_ga ³Π_u de la molécula de C₂. Para rellenar la Tabla 1 con los datos correspondientes a las transiciones con Δ=-1, 0, 1, utilizad los datos del fichero adjunto, representado en la Figura 3. A partir de las primeras diferencias de las cabezas de banda obtener los valores promedios de las diferencias <Δν_v”,v”+1> y <Δν_v’,v’+1> . Representar estos valores promedio en función del número cuántico vibracional (” o ’) y realizar un ajuste a la ecuación (2) con sólo dos constates vibracionales, con el fin de obtener  y para los estados electrónicos d³Π_g y  a³Π_u de la molécula de C₂  y comparar con los valores tabulados. Representar en la misma figura el ajuste realizado.

 

Tabla 1: tabla de Deslandres para las bandas vibracionales con Δ=-1, 0, 1, correspondiente a la transición electrónica d ³Π_ga ³Π_u de la molécula de C₂.

 

v’=0

v’=1

v’=2

v’=3

v’=4

v’=5

<Δνv”,v”+1>

v”=0

19352.3

1759.1

21111.4

1613.0

v”=1

17739.3

v”=2

v”=3

v”=4

v”=5

<Δνv’,v’+1>

Cálculo de la energía de disociación D₀ de los estados d³Π_g y a³Π_u del C₂.

Cuando se conocen las frecuencias vibracionales de diferentes transiciones entre niveles vibracionales adyacentes =0↔=1, =1↔=2, =2↔=3, ... se puede utilizar una técnica gráfica conocida como extrapolación de Birge-Sponer para obtener una energía de disociación D₀, referida al nivel vibracional más bajo, de un estado electrónico. El método gráfico de Birge-Sponer se basa en que la suma de los sucesivos intervalos ΔG_v+1/2 (ecuación 2) desde el nivel de punto cero de energía hasta el límite de disociación es la energía de disociación:

                                                                                                                                       (3)

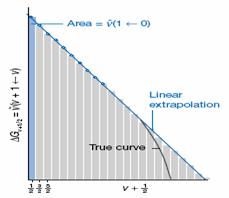Si se representa ΔG_v+1/2 frente a  +1/2, el área bajo la curva es dicha suma y dará la energía de disociación D₀. Los términos sucesivos ΔG_v+1/2 decrecen casi linealmente con +1/2 (Figura 5) con lo que si se extrapola linealmente dicha gráfica se obtiene un valor aproximado de la energía de disociación D₀ , superior al valor real.

Figura 5: Extrapolación de Birge-Sponer. El área bajo la curva es igual a la energía de disociación D₀.

 

Ejercicio 2: Teniendo en cuenta los datos de la tabla de Deslandres del Ejercicio 1 (Tabla 1) representar ΔG_v’+1/2frente a  ’+1/2 para obtener por extrapolación lineal la energía de disociación del estado superior d³Π_g  de la molécula de C₂. Comparar con el valor calculado como

                                                                                                                                          (4)

donde para el cálculo de la energía de disociación D_e referida al mínimo de la curva de energía potencial se ha utilizado la relación de Kratzer. Obtener G(0) con las constantes dadas en la Tabla 3. Representar ΔG _v”+1/2 frente a  ”+1/2 para obtener por extrapolación lineal la energía de disociación del estado inferior a³Π_u  de la molécula de C₂. Comparar con el valor calculado utilizando la ecuación (4).

Análisis de las intensidades de las bandas vibracionales del C₂: d³Π_ga³Π_u

 

La intensidad de una banda vibracional ’- ” en emisión se puede aproximar como

                                                                                                                                               (5)

donde C es una constante, N_v’ es la población del estado excitado desde donde se produce la emisión y

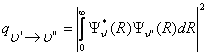                                                                                                                                           (6)

es el factor de Franck-Condon. Para transiciones electrónicas, las funciones de onda vibracionales Ψ_v(R) corresponden a estados electrónicos diferentes. Cuanto mayor es el solapamiento de las funciones de onda mayor es la intensidad de la banda. Como ejemplo, en la Figura 6 se muestran las curvas de energía potencial y algunas funciones densidad de probabilidad  para los estados electrónicos B¹Π_u y X¹Σ⁺ de la molécula de Na₂.

 

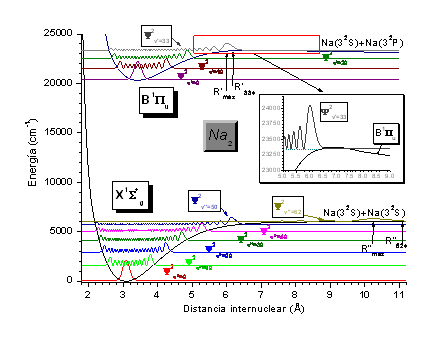
Figura 6: Curvas de energía potencial y funciones densidad de probabilidad de algunos estados de la molécula de Na₂.

 

A presión atmosférica se producen un gran número de colisiones y las moléculas en estados electrónicos excitados se redistribuyen siguiendo una distribución tipo Boltzmann:

 

                                                                                                                (7)

donde N₀ es la población del nivel vibracional más bajo (que se puede tomar como 1), G()-G(0) es la diferencia de energía vibracional entre los estados con número cuantico vibracional  y el nivel vibracional más bajo (=0) y T es la temperatura absoluta.

 

 

 

Tabla 2: Factores de Franck-Condon (Ecuación 6) para algunas bandas vibracionales del espectro electrónico d³Π_ga³Π_u de la molécula de C₂.

 

v”	v’=0	v’=1	v’=2	v’=3	v’=4	v’=5
0	0.7294	0.2442	0.02715	0.001153	1.138E-5	1.028E-6
1	0.2155	0.3452	0.3641	0.0711	0.003072	1.055E-5
2	0.04553	0.286	0.1383	0.4238	0.1011	0.0045
3	0.007771	0.0932	0.2607	0.04305	0.4468	0.1433
4	0.001263	0.02393	0.144	0.2122	0.009505	0.4317
5	1.896E-4	0.005776	0.04983	0.1596	0.1566	8.132E-4
6	3.731E-5	0.001328	0.01248	0.06215	0.1581	0.1107
7	2.256E-5	3.281E-4	0.002952	0.01955	0.08192	0.1584
8	1.554E-5	5.921E-5	6.743E-4	0.005536	0.03042	0.09407
9	3.005E-6	2.328E-6	1.385E-4	0.001503	0.009449	0.03833
10	9.642E-7	1.158E-6	2.147E-5	3.58E-4	0.002644	0.01308
11	6.308E-6	1.02E-6	2.378E-6	5.804E-5	6.153E-4	0.00387
12	4.256E-6	8.552E-9	3.926E-7	4.986E-6	1.098E-4	9.261E-4

Ejercicio 3: Tomar como intensidad experimental de las bandas la altura de la cabeza de banda de la Figura 3. Comparar la intensidad experimental con la intensidad teórica obtenida mediante la ecuación (5) para las bandas vibracionales indicadas en la Figura 3 (banda electrónica d³Π_ga³Π_u de la molécula de C₂). Para el cálculo de la población del estado excitado (ecuación 7) tomar para la temperatura de la llama T=2000 K y normalizar, las intensidades teórica y experimental, a la unidad para la banda más intensa (’=0-”=0).

Análisis de la estructura rotacional de la banda del CH: B²Σ ^-X²Π (v’=0-v”=0)

            Las curvas de energía potencial se representan en la Figura 4 (Hüber K.P y Herzberg  G., Constants of Diatomic Molecules. Van Nostrand-Reinhold. New York. 1979). De acuerdo con la regla de selección ΔΛ=0,±1, las transiciones A²Δ X²Π y B²Σ ^-X²Π  están permitidas, tal y como se observa en el espectro experimental (Figuras 1 y 2). El espectro de la banda vibracional ’=0-”=0 correspondiente a la transición electrónica: B²Σ ^-X²Π de la molécula de CH se muestra en las dos figuras de la introducción y en la Figura 7, en la zona entorno a 380-400 nm (25900-24800 cm^-1). Al tratarse de una molécula con una masa reducida pequeña (hidruro) las constantes rotacionales tienen valores grandes (ver Tabla 3) con lo que la estructura rotacional se puede resolver. El estudio detallado de la estructura rotacional de una banda ²Σ ^-2Π no será considerado aquí (para esta banda electrónica, los estados corresponden al caso de acoplamiento (b) de Hund; para cada valor de N hay dos niveles de energía casi degenerados con J=N±½). Sin considerar el espín electrónico (J=N), la energía rotacional se puede expresar como (despreciando el término de distorsión centrífuga y términos de orden superior)

        donde                                                            (8)

siendo B_e(=h/8π²cμR_e²) , α_e las constantes rotacionales en cm^-1. Para una banda electrónica: Σ↔Π, la regla de selección entre estados rotacionales es: ΔJ=J’-J”=0, ± 1. Así tenemos 3 ramas; la rama Q (ΔJ=0), cuyas líneas vienen dadas por

;                 J=J”=1, 2, 3, ...       (9) 

 

donde ν₀=T_e’- T_e”+G’(v’)-G”(v”) es el origen de banda (línea inexistente) y B_v’ y B_v” son las constantes rotacionales de los estados excitado y fundamental, respectivamente. Los números de onda de las líneas de la rama R (ΔJ=+1) vienen dados por

; J=J”=0,1,2,... (10)

  

Los números de onda de las líneas de la rama P (ΔJ=-1) vienen dados por

;                  J=J”=1, 2, 3,...      (11)

 

Las primeras  líneas de la rama P son P(1), P(2), P(3), ... donde se sigue la notación: RPQ(J”).

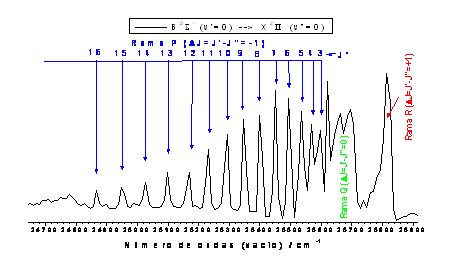
Figura 7: Emisión debida a la transición  B²Σ ^--> X²Πde la molécula de CH y asignación de algunas líneas de la rama P.

 

Como vemos en la Figura 7, la banda está degradada hacia el rojo, formándose la cabeza de banda con las líneas de la rama R. El espaciado entre líneas consecutivas de la rama P viene dado por:

 

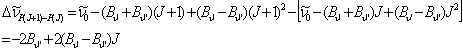            J=J”=1, 2, 3,...    (13) 

Ejercicio 4: A partir del espaciado medido de las líneas de la rama P indicadas en la Figura 7; Representar dichas diferencias en función de J=J” y del ajuste por mínimos cuadrados a la ecuación (13), determinar las constantes rotacionales B_v”=0 y B_v’=0. Comparar con los valores obtenidos mediante la ecuación (9) empleando las constantes de la Tabla 3.

(Pincha aqui si quieres la tabla con los puntos y aqui si quieres la figura en pdf, en postscript o en gif)

Teniendo en cuenta que el número de moléculas N_J en un estado rotacional J, en un sistema en equilibrio térmico a una temperatura T, se puede tomar como

 

                                                                                                            (14)

 

es fácil obtener el nivel rotacional más poblado, que corresponde con el máximo [(dN_J/dJ)=0], obteniéndose

 

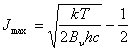                                                                                                                           (15)

donde T es la temperatura absoluta en K y B_v es la constante rotacional en cm^-1. A partir del valor medido experimental para J_max (Figura 7), y del valor de B₀, para la banda v’=0-v”=0, B²Σ ^- ->X²Π del CH; Determinar la temperatura de la llama empleando la ecuación 15.

 

Tabla 3:Contantes espectroscópicas experimentales para las moléculas consideradas (Hüber K.P y Herzberg  G., Constants of Diatomic Molecules. Van Nostrand-Reinhold. New York. 1979.)

Molécula	Estado Electrónico	Te cm-1	cm-1	cm-1	cm-1	cm-1	Be cm-1	αe cm-1	γe cm-1
16O 1H	X2Π	0	3737.761	84.8813	-1.7915	0.32362	18.9108	0.7242	0.00706
OH	A2Σ+	32684.1	3178.86	92.917	0.5409	-0.02134	17.358	0.7868	-0.016
12C 1H	X2Π	0	2858.5	63.02			14.457	0.534
CH	A2Δ	23189.8	2930.7	96.65			14.934	0.697
CH	B2Σ-	26070	2251	231			13.3815	1.4827
12C 2	a3Πu	716.2	1641.35	11.67			1.6324	0.01661
C2	d3Πg	20022.5	1788.22	16.440	0.5067		1.7527	0.01608